গণিত সুন্দর, প্রোগ্রামিং সুন্দর

বৃহস্পতিবার, আগস্ট ৮, ২০১৯শুক্রবার, আগস্ট ৯, ২০১৯ আব্দুল্যাহ আদিল মাহমুদ

গণিত সুন্দর। কথাটি মুখে বললেই তো হবে না। প্রমাণ চাই। তবে কথাটা প্রমাণ ছাড়াই বুঝেছিলেন পিথাগোরাস, গ্যালিলিওরা। তাই তো সবকিছুকে সংখ্যা দিয়ে প্রকাশ করতে চেয়েছিলেন পিথাগোরাস। আর গ্যালিলিওর গণিত নিয়ে সুন্দর কথাটা তো বারবার শোনার মতো-

“আমাদের মহাবিশ্ব আসলে বিরাট এক গ্রন্থ। এর পরতে পরতে মিশে আছে দর্শন। গ্রন্থটা আমাদের চোখের সামনেই পড়ে আছে। কিন্তু একে বুঝতে হলে এর ভাষা আয়ত্ত করা চাই। সেই বর্ণগুলো চেনা চাই,যা দিয়ে লেখা হয়েছে এই বই। এটি লেখা হয়েছে গণিতের ভাষা দিয়ে,আর এর বর্ণমালা হলো ত্রিভুজ,বৃত্ত ও অন্যান্য জ্যামিতিক চিত্রগুলো। এগুলো বাদ দিয়ে বইটির একটি শব্দও বোঝা সম্ভব নয়।“

II Saggiatore(1623)

আমরা ফুলের সৌন্দর্য দেখে বিমোহিত হই। এঁকে-বেঁকে বয়ে চলা নদীর দৃশ্য আমাদের মুগ্ধ করে। পাহাড়-নদীর অভিসারের দিকে নির্নিমেষ নয়নে তাকিয়ে থাকতে ইচ্ছে হয়। এই সবগুলো সৌন্দর্যের পেছনে লুকিয়ে আছে গণিত। তাই তো গ্যালিলিওর আরেকটি উক্তি, ‘ঈশ্বর মহাবিশ্ব লিখেছেন গণিতের ভাষা দিয়ে।‘

সুন্দরতম প্রাণি মানুষের কথাই একবার ভাবি না! অথবা ভাবুন আপনার পছন্দের অন্য কোনো প্রাণির কথাই। ‘বার্ডস অব প্যারাডাইস’ পাখিটির দিকে কার না তাকিয়ে থাকতে ইচ্ছে হয়! এদের এই সৌন্দর্যের পেছনে লুকিয়ে আছে ডিএনএ-এর সিকুয়েন্স। এটিজিসির (ATGC) বিন্যাস। গণিত ও প্রোগ্রামিং। এমনকি গণিত লুকিয়ে আছে ভালোবাসার মধ্যেও। কথাটা শুনে গণিতের প্রতি একটু শ্রদ্ধা হয়তোবা জন্মায়। কিন্তু ঠিক বিশ্বাস হতে চায় না যেন!

তাহলে ১নং ছবিটার দিকে একটু চোখ বড় বড় করে তাকানো যাক। ছবিতে একটি প্রজাপতি দেখা যাচ্ছে। অন্তত প্রজাপতির নকশা বললে আশা করি কেউ-ই আপত্তি করবেন না। দেখুন ২য় ছবিটাও।

মজার ব্যাপার হলো এই ছবিগুলো ফটোশপ বা ইলাস্ট্রেটর দিয়ে তৈরি নয়। নয় গুগল সার্চে পাওয়া। সম্পূর্ণ গাণিতিক সমীকরণ আর প্রোগ্রামিং-এর সাহায্যে তৈরি। এজন্যই গণিতের সাথে শিরোনামে প্রোগ্রামিং কথাটা উল্লেখ করা।

গণিত নিয়ে যখন আলোচনা চলছেই, এখন হোক পরে হোক কিছু বিদ্ঘুটে(?) কিছু সমীকরণ দেখতে হবেই। তা শুভকাজে (অবশ্যই এটা শুভকাজই) দেরি করতে নেই। তাহলে দেখে নেই কোন সমীকরণ আর কোডিং-এর ফসল এমন ছবি!

এই ছবি আঁকতে ব্যবহার করেছি বাটারফ্লাই কার্ভের পরামিতিক সমীকরণ। এমনিতে সমীকরণটার পোলার (polar) রূপ এ রকম-

$latex r={{e}^{{sin\theta }}}-2\cos \left( {4\theta } \right)+~si{{n}^{5}}\left( {\frac{{2\theta -\pi }}{{24}}} \right)$

তবে এমন সমীকরণ থেকে অনেক সময় সরাসরি কার্ভের সঠিক রূপ পাওয়া যায় না। এই সমীকরণের পরামিতিক রূপ আবার খুব শক্তিশালী। পরামিতিক সমীকরণের চমৎকার দিক নিয়ে অন্য সময় না হয় আবার জানব। আপাতত জেনে রাখি, পরামিতিক সমীকরণ আমরা ব্যবহার করি দুটো চলকের সম্পর্ককে তৃতীয় অন্য একটি চলক (সাধারণত t) দিয়ে দুটো আলাদা সমীকরণ আকারে প্রকাশ করতে।

তো বাটারফ্লাই বা প্রজাপতি কার্ভের পরামিতিক সমীকরণ হলো এ দুটি:

$latex x=\text{sin}\left( t \right)\left( {{{e}^{{cost}}}-2\cos \left( {4t} \right)-si{{n}^{5}}\left( {\frac{t}{{12}}} \right)} \right)$

$latex y=\text{cos}\left( t \right)\left( {{{e}^{{cost}}}-2\cos \left( {4t} \right)-si{{n}^{5}}\left( {\frac{t}{{12}}} \right)} \right)$

যেখানে $latex 0\le ~t\le 12\pi $

এটাকে এখন R প্রোগ্রামিং দিয়ে প্লট করে নিলেই হলো। কঠিন কাজ সহজে করে ফেলতে R এর জুড়ি তো পাওয়া যাবেই না। নিচের কোডটা প্রথম ছবির। দ্বিতীয় ছবির কোডও একই ধরনের।

t <- seq(0, 12*pi, length.out = 10000)
x <- sin(t)*(exp(cos(t))-2*cos(4*t)-((sin(t/12))^5))
y <- cos(t)*(exp(cos(t))-2*cos(4*t)-((sin(t/12))^5))
plot(x,y, col="blue", type="l")

অনেকে বলেন, ভালোবাসা কোনো সমীকরণ মেনে চলে না। তারা যে না বুঝে ভুল বলেন তার প্রমাণ আমরা এক্ষুণি দেখবো। অবশ্য ক্রিস্টোফার নোলানের অবিস্মরণীয় অবদান (আসলে নোবেলজয়ী পদার্থবিদ কিপ থর্নের স্বপ্নের ফসল) ইন্টারস্টেলার মুভি দেখলে আপনি ভাবতে বাধ্য হবেন ভালোবাসা স্থান, কাল, মাত্রা কিছুই মানে না। তবে সাথে সাথে দেখবেন, বিজ্ঞানী মেয়ের মহাবিশ্বের রহস্যভেদে কাজে লাগে ওয়ার্মহোলভেদী নভোচারী বাবার বহু আলোকবর্ষ দূরের ভালোবাসা থেকে উৎসারিত ভিন্ন মাত্রা থেকে পাঠানো সমীকরণই। কিন্তু শুধু ভালোবাসা দিয়ে আসলেই কি তথ্য প্রেরণ সম্ভব? এ প্রশ্নের জবাব পরিসংখ্যানকেই দিতে হবে এমন কোনো কথা নেই (চাইলে পারবে না এমন কিছু পরিসংখ্যানে নেই যদিও)। তবে ভালোবাসা যে সমীকরণ মেনে চলে সেটা আমরা দেখতে পারি।

তাহলে দেখা যাক ভালোবাসায় কীভাবে গণিত আসছে। বা উল্টো করে বলা যায়, গণিতের মধ্যে কীভাবে ভালোবাসা প্রবেশ করল। এটা বিস্তারিত বলার সুযোগ এখানে হবে না। আমরা শুধু সমীকরণগুলো দেখব। আরও জানতে আপনাকে পড়তে হবে ব্যাপন বিজ্ঞান ম্যাগাজিনের সেপ্টেম্বর-অক্টোবর, ২০১৭ সংখ্যা। ৪ নং ছবিতে দেখুন সমীকরণ থেকে পাওয়া ভালোবাসা।

অবশ্যই এমন ছবি আঁকতে আপনাকে চিত্রকর বা ডিজাইনার হতে হবে এমন কোনো কথা নেই। গণিত আর প্রোগ্রামিং পারলেই হবে। অতএব জন ন্যাশের মতো গণিতবিদ হয়ে গেলেই যে মন থেকে ভালোবাসা হারিয়ে যাবে এমনটি ভাবার কোনো সুযোগ নেই। নিচের সমীকরণগুলো ঠিকঠাক করে এঁকে ফেলতে পারলেই কেল্লা ফতে!

$latex y=-3\sqrt{{1-\sqrt{{\frac{{\left| x \right|}}{2}}}}}$

যেখানে x এর ডোমেন -২ থেকে ২। এটা দিয়ে ভালোবাসের একাংশ পাবেন। পূর্ণ ভালোবাসা পেতে হলে আরও দুটি সমীকরণ লাগবে।

$latex y=\sqrt{{1-{{{\left( {x-1} \right)}}^{2}}}}$

$latex y=\sqrt{{1-{{{\left( {x+1} \right)}}^{2}}}}$

অনেকেই বুঝতে পেরেছেন, পরের দুটি আসলে বৃত্তের সমীকরণ, যেখান থেকে আমরা শুধু অর্ধবৃত্তাংশটুকু নিচ্ছি। এখন সমীকরণগুলোর এই রূপ দিয়ে আপনি ভালোবাসাকে সরাসরি নাও খুঁজে পেতে পারেন। সেটা পেতে হলে আপনাকে অন্তত প্রথম সমীকরণটিকে পরামিতিক বানিয়ে নিতে হবে।

ধরি, $latex x=2t$

তাহলে $latex y=-3\sqrt{{1-\sqrt{t}}}$

বাকি দুটো সমীকরণ এভাবে থাকলেই চলবে।

এবার এদেরকে R দিয়ে এঁকে ফেলতে চাইলে এই কোড রান দিয়ে ফেলুন:

t=seq(-1,1, length.out=1000)
x=c(2*t, -2*t)
y=-3*sqrt(1-sqrt(t))
plot(x,c(y,y),col="red", ylim=c(-3, 1.5), type="l", lwd=10)
curve(sqrt(1-(x-1)^2),add=TRUE, col="red", pch=19, lwd=10)
curve(sqrt(1-(x+1)^2),add=TRUE, col="red", pch=19, lwd=10)

শামুকের খোলসের সর্পিল, রঙিন আকৃতি মুগ্ধ করে না এমন লোক খুঁজে পাওয়া যাবে না। কিংবা চিন্তা করুন আনারসের সুন্দর প্যাঁচগুলো। কী দারুণভাবেই না সেটা নিচ থেকে উপরে উঠে যাচ্ছে। চিলকেই বা কে শিখিয়েছে সর্পিল পথে নেমে শিকার ধরতে। সূর্যমুখী ফুল কোথায় পেল এমন দারুণ নকশা! এইমাত্র যেগুলোর কথা বললাম তার সবগুলো মেনে চলে ফিবোনাচি সংখ্যা। দেখতে-শুনতে সংখ্যাগুলোকে হয়তোবা যথেষ্ট দৃষ্টিকটু ঠেকে। কতগুলো একঘেঁয়ে সংখ্যা। প্রতিটার সাথে আগেরটা যোগ করে পরের সংখ্যা। এর মধ্যে আর এমন কী?

বিশ্বাস করা কঠিন হলেও ৫ নং ছবির শামুকের খোলসের সর্পিল নকশা কিন্তু অবচেতনভাবে মেনে চলে গণিত। বুঝতেই পারছেন, এখানে ফিবোনাচি সংখ্যার গুণগান গাওয়ার জন্য প্রস্তুত হচ্ছি। চলুন দেখা যাক কীভাবে ফিবোনাচিরা এই নকশার জন্ম দেয়।

সংখ্যাগুলো হলো এমন:

১ ১ ২ ৩ ৫ ৮ ১৩ …

পরপর দুটি যোগ করে পরেরটি। এটা থেকে সর্পিল বিন্যাস পেতে একটা কাগজে ১ একক বাহুর একটি বর্গ আঁকুন। পরের ফিবোনাচি সংখ্যাও ১। আগের বর্গের পাশে আরেকটি এক একক বাহুর বর্গ আঁকুন। এবার এ দুটি বর্গের ওপরে (নিচে আঁকলেও দুনিয়া ধ্বংস হবে না!) ২ এককের একটি বর্গ আঁকুন। এই তিনটি বর্গের পাশে আঁকুন ৩ এককের আরেকটি বর্গ। এভাবে এগিয়ে চলুন।

এভাবে যেতে থাকলে পাবেন নিচের আয়তক্ষেত্রটি।

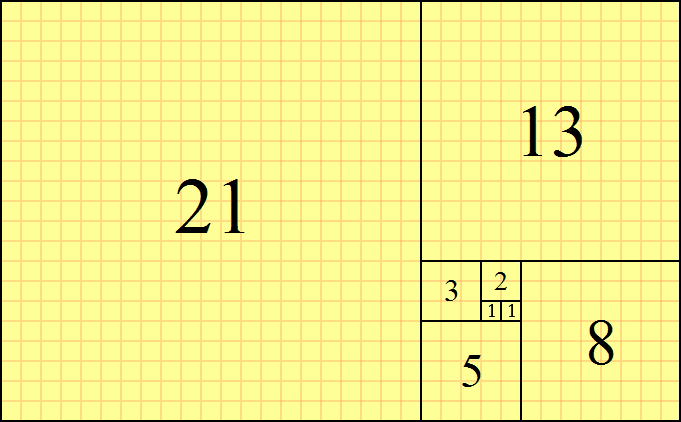
এবার ক্রমান্বয়ে ছোট থেকে বড় বর্গের দিকে বর্গের কর্ণ বরাবর সর্পিল বাহু এঁকে যেতে থাকলেই আমরা পাব দারুণ একটি সর্পিল রেখা।

আরে! এই রেখাই তো পাওয়া যায় শামুকের খোলসে। আনারস ফলে। সূর্যমুখী ফুলে।

এমন আরও কিছু ছবি দেখে রাখলে ক্ষতি নেই। ফিবোনাচির ধারণাকেই একটু রূপভেদ ঘটিয়ে আঁকা ছবি। একটু ভাবলেই দেখবেন, ভেতরে ভেতরে সূর্যমুখীতে এমন কিছুই থাকে আসলে।

বাস্তব জগতে গণিতের ছড়ি ঘোরানোর খুব সামান্য অংশই আমরা দেখলাম। গ্যালিলিও মহাবিশ্বকে গণিতে গড়া বলে নিশ্চয় এতটুকু ভুল বলেননি। আসলেই তো সবকিছু গণিত মেনে চলছে। হ্যাঁ, কখনও কখনও আমরা নিখুঁতভাবে মেনে চলতে দেখি না। শেয়ারবাজার কিংবা আবহাওয়া কি আর গণিত মেনে চলে? হয়তো চলে না, তবে সেগুলোকেও আমরা পরিসংখ্যানিক পদ্ধতি দিয়ে মডেল করতে পারি। বের করতে পারি অবিন্যস্ততার আড়ালে লুকিয়ে থাকা অন্তর্নিহিত নকশা। পেতে পারি অনিয়মের মাঝে নিয়ম। এ জন্যেই তো পরিসংখ্যান ব্যবহার করে জন্ম হয়েছে ডেটা মাইনিং, মেশিন লার্নিং-এর মতো শাখাগুলোর। পরিসংখ্যানের প্রিন্সিপাল কম্পোনেন্ট বা ফ্যাক্টোর অ্যানালাইসিস কিংবা ক্লাস্টারিং অ্যালগরিদমগুলো তো ভেতরে ভেতরে এই কাজটাই করে। লুক্কায়িত নকশার সন্ধান।

মহাবিশ্বের সবকিছুর এমন নিয়ম জেনে ফেলার সন্ধানে আছে বিজ্ঞানীরা। সেই সোনার হরিণ ধরনের তত্ত্বের নাম থিওরি অব এভরিথিং। কাজটা যতটা পদার্থবিদদের ততটাই কিন্তু আবার গণিতবিদদের। পরিসংখ্যানবিদদের।

আইনস্টাইন, হকিংদের স্বপ্নের এই তত্ত্ব নিয়ে নিরন্তন স্বপ্ন দেখেন বিজ্ঞানীরা। তাঁদের মতে সেই তত্ত্ব পাওয়া গেলে জানা যাবে ঈশ্বরের মন। আইনস্টাইন তো বলেছিলেনই, মহাবিশ্বের সূত্রগুলো আসলে ঈশ্বরের মনের বহিঃপ্রকাশ। আর ঈশ্বর সেই বহিঃপ্রকাশ যে গণিত দিয়ে ঘটিয়েছেন, মহাবিশ্বের পরতে পরতে গণিত লুকিয়ে রেখেছেন তার কিঞ্চিত নমুনা তো আমরা দেখলামই।

পুনশ্চঃ প্রজাপতি, ভালোবাসা বা এমন আরও কী কী কার্ভ আছে জানতে ও আঁকতে সূত্রে উল্লিখিত ৯নং লিঙ্কটা দেখুন।

সূত্রঃ