প্রথম অঙ্কের আইন- Benford’s law
প্রথম অঙ্কের আইন- Benford’s law
আপনি কি মনে করেন, শুধুমাত্র একটি ডেটাসেট দেখে, অ্যাকাউন্টিং ডেটা বা কোনো ডেটাসেট ম্যানিপুলেট করা হচ্ছে কিনা তা শনাক্ত করা সম্ভব? বা একটি বীমা দাবি জালিয়াতি বের করা সম্ভব শুধু ডেটা দেখেই? অথবা কিছু পণ্যের মানের ফলাফলকে পাল্টানো হচ্ছে কি না, তা যাচাই সম্ভব কোনো এনালাইসিস না করেই? বেনফোর্ডের আইনের মাধ্যমে, খুব সাধারণ বিশ্লেষণের মাধ্যমে ম্যানিপুলেটেড ডেটা শনাক্ত করা যায়। তবে এই নীতিটি প্রয়োগ করে শুধু মাত্র naturally occurred or naturally originated data এর ম্যানিপুলেশন বের করা সম্ভব।
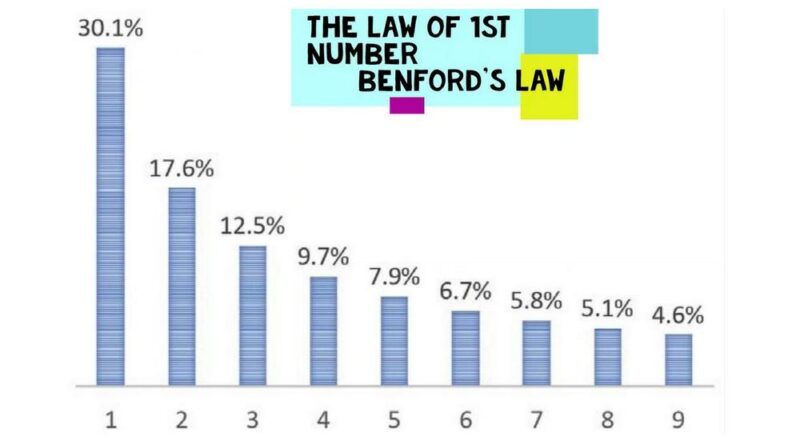
বেনফোর্ডের আইন (as the law of anomalous numbers, or the first-digit law) যা অসামঞ্জস্যপূর্ণ সংখ্যার আইন বা প্রথম অঙ্কের আইন নামেও পরিচিত। এটি মূলত একটি পর্যবেক্ষণ যে, অনেক বাস্তব-জীবনের ডেটাসেটে লিডিং ডিজিট বা প্রথম সংখ্যাটি ছোট হয়ে থাকে। বেনফোর্ডের আইন বলে, অনেক সংখ্যার প্রথম সংখ্যাগুলি একটি ডেটাসেট জুড়ে এলোমেলোভাবে এবং সমানভাবে ঘটে না। যদি সংখ্যাগুলি (1-9) সমানভাবে বিস্তৃত হয়, তবে তারা প্রতিটি সময়ের প্রায় 11.1 % থাকবো। কিন্তু বেনফোর্ডের আইন অনুসারে, প্রথম অঙ্কে 1 থাকার সম্ভাবনা 11.1% নয়। বাস্তবে, এটি প্রায় 30%, যা 11.1% থেকে অনেক বেশি। প্রথম অঙ্কে 2 হওয়ার সম্ভাবনা 17.6% এ নেমে আসে। এটি 1-এর সংঘটনের তুলনায় অনেক কম। প্রথমে সংঘটনের সম্ভাবনা 9-এর জন্য 4.6%-এ কমে যায়, যা প্রত্যাশিত 11.1%-এর চেয়ে অনেক কম। সুতরাং, বেনফোর্ডের আইন অনুসারে একটি ডেটা সেটের, সাংখ্যিক ডেটার 4.6% পর্যবেক্ষণে ১ম সংখ্যা হিসাবে 9 থাকবে।
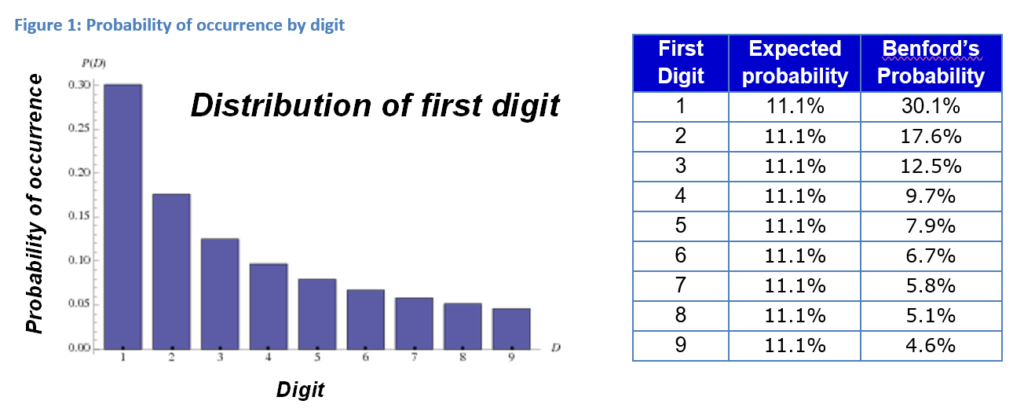
বেনফোর্ডের আইনটি দ্বিতীয়, তৃতীয় এবং পরবর্তী অগ্রণী সংখ্যাগুলি এবং নির্দিষ্ট সংখ্যার সংমিশ্রণের সম্ভাব্যতাগুলি কী হবে সে সম্পর্কেও ভবিষ্যদ্বাণী করতে ব্যবহার করা যেতে পারে। বেনফোর্ডের আইন প্রতিটি সংখ্যার সেটের ক্ষেত্রে প্রযোজ্য নয়, তবে এটি সাধারণত প্রাকৃতিকভাবে সংঘটিত সংখ্যার বড় ডেটা সেটগুলিতে প্রযোজ্য হয়। যেমন;
- কোম্পানির শেয়ার বাজার মূল্য
- রাজ্য এবং শহরের জনসংখ্যা সহ ডেমোগ্রাফিক ডেটা,
- আয়কর তথ্য,
- গাণিতিক টেবিল (লগারিদমের মতো)
- নদী নিষ্কাশনের হার,
- বৈজ্ঞানিক তথ্য ইত্যাদি।
আইনটি সাধারণত সেই সব ডেটা সেটের ক্ষেত্রে প্রযোজ্য হয় না, যেগুলির ন্যূনতম এবং সর্বোচ্চ উল্লেখ থাকে, যেমন সুদের হার বা ঘন্টার মজুরি। যদি সংখ্যাগুলি স্বাভাবিকভাবে ঘটানোর পরিবর্তে বরাদ্দ করা হয়, তবে তারাও এই আইন অনুসরণ করবে না। নির্ধারিত নম্বররের উদাহরণরের মাঝে রয়েছে: জিপ কোড, টেলিফোন নম্বর এবং সামাজিক নিরাপত্তা নম্বর।
যেমনঃ বাংলাদেশের মোবাইল নম্বর গুলো শুরু হয় ০১ দিয়ে এবং ৩য় ডিজিটটি সাধারণত অপারেটর এর কোড। কিন্তু আমরা যদি মোবাইল নম্বরের ৪র্থ ডিজিট নিয়ে বিশ্লেষণ করি, তাহলে একটি বড় ডেটাসেটের জন্য এই ঘরের সংখ্যাটি বেনফোর্ডের নীতি মেনে চলার কথা।
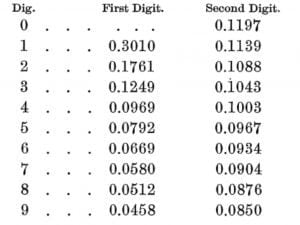
এটিকে বেনফোর্ডের আইন বলা হলেও, তিনি ঘটনাটি শনাক্তকারী বা বিশ্লেষণকারী প্রথম ব্যক্তি ছিলেন না। জ্যোতির্বিজ্ঞানী সাইমন নিউকম্ব (আমেরিকান গাণিতিক সোসাইটির ভবিষ্যত সভাপতি, ১৮৮১) লগারিদম টেবিল দেখার পরে এই আইনের ভিত্তি স্থাপন করেছিলেন। তিনি লক্ষ্য করলেন যে, প্রথম পৃষ্ঠাগুলি পরবর্তী পৃষ্ঠাগুলির তুলনায় বেশি জীর্ণ এবং ধোঁয়াটে। নিউকম্ব তারপরে সিদ্ধান্তে আসেন যে, “প্রথম স্থানের অঙ্কটিতে অন্য যেকোনো অঙ্কের চেয়ে প্রায় 1 বেশি সংখ্যক বার থাকে” এবং প্রাকৃতিক সংখ্যায় বিভিন্ন অঙ্কের ব্যবহারের ফ্রিকোয়েন্সি নোটে তার ফলাফল প্রকাশ করেছেন, যা দ্য আমেরিকান জার্নাল অফ ম্যাথমেটিক্স-এ প্রকাশিত হয়েছিল। Newcomb ১ম এবং ২য় সংখ্যার সম্ভাব্যতার জন্য একটি টেবিল অন্তর্ভুক্ত করেছিলেন, তা হলো d:
পরে প্রখ্যাত ফরাসি গণিতবিদ হেনরি পয়নকারে এই ধারণাটিকে আরও বিকশিত করেছিলেন, Répartition des décimales dans une table numérique (সংখ্যাসূচক সারণিতে দশমিকের বন্টন) এ। আইনটি জেনারেল ইলেকট্রিক কোম্পানির পদার্থবিজ্ঞানী ফ্রাঙ্ক বেনফোর্ডের কাছ থেকে নামকরণ করা হয়েছে, তিনি নিউকম্বের অনুসন্ধানগুলি পুনরায় আবিষ্কার করেছিলেন এবং এটি বিখ্যাত করেছিলেন। বেনফোর্ড’ আইনটি দেখানোর জন্য বিভিন্ন নম্বর সেট ব্যবহার করেছিলেন। তিনি ২০টি বিভিন্ন ডেটা সেট থেকে ২০,২২৯ টি বিশ্লেষণের করেছেন, যার মধ্যে ছিল:
- রাস্তার ঠিকানাগুলির একটি তালিকা,
- হাজার হাজার রাসায়নিকের জন্য আণবিক ওজন এবং নির্দিষ্ট তাপ
- ৩৩৫টি নদীর উপরিভাগ এলাকার ডেটা
- গাণিতিক ক্রম
- রিডার্স ডাইজেস্টের একটি সমস্যা।
বেনফোর্ড আমেরিকান ফিলোসফিক্যাল সোসাইটি (1938) এর The Law of Anomalous Numbers প্রবন্ধে তার ফলাফল প্রকাশ করেছেন। উদাহরণ হিসেবে, তিনি রিডার্স ডাইজেস্টে নিম্নলিখিত শতাংশগুলি দিয়েছিলেন(total count, 308 instances):
- 1 = 33.4%
- 2 = 18.5%
- 3 = 12.4%
- 4 = 7.5%
- 5 = 7.1%
- 6 = 6.5%
- 7 = 5.5%
- 8 = 4.9%
- 9 = 4.2%
বেনফোর্ড নিজেই উল্লেখ করেছেন যে, একটি পৃথক(একক) ডেটা সেট, এই আইনের সাথে মানানসই নাও হতে পারে। তবে বিপুল সংখ্যক ডেটা এর গড় বা মিশ্রণ এই নীতি অনুসরণ করবে।

ব্যবহারসমূহ:
বেনফোর্ডের আইনের প্রয়োগ হয় জালিয়াতি এবং ত্রুটি সনাক্তকরণে। এটি প্রত্যাশিত যে, একটি বৃহৎ ডাটা সেট এই আইন অনুসরণ করবে। তাই হিসাবরক্ষক, নিরীক্ষক, অর্থনীতিবিদ এবং কর পেশাদারদের একটি বেঞ্চমার্ক আছে যে, একটি ডাটা সেটে কোনো নির্দিষ্ট সংখ্যা থাকার স্বাভাবিক মাত্রা কী বা কত হতে পারে।
- 1990-এর দশকের শেষার্ধে, হিসাবরক্ষক মার্ক নিগ্রিনি দেখতে পান যে, বেনফোর্ডের আইন বানোয়াট ট্যাক্স রিটার্নের জন্য একটি কার্যকর red-flag test হতে পারে; সত্যিকারের ট্যাক্স ডেটা সাধারণত বেনফোর্ডের আইন অনুসরণ করে, যেখানে অবাস্তব ট্যাক্স রিটার্ন, যেমন Maddoff scam দ্বারা বানোয়াট ডাটা, প্রত্যাশিত বেনফোর্ড বন্টন নীতি মানে না (Frunza, 2015)।
- এই আইনটি 2001 সালে গ্রিস থেকে অর্থনৈতিক তথ্য বিশ্লেষণের জন্য ব্যবহার করা হয়েছিল, এটা বের করতে যে, দেশটি ইউরোপীয় ইউনিয়নে যোগদানের জন্য তাদের Economic data তে হেরফের করেছে কি না।
- এই আইন ব্যবহার করে Ponzi schemes (an investment fraud that pays existing investors with funds collected from new investors) সনাক্ত করা যেতে পারে।
উপসংহারে বলা যায়, এটা সুস্পষ্ট বলে মনে করা উচিত যে শুরুতে অন্য যেকোনো সংখ্যার তুলনায় “1” ই বেশি হবে, কারণ এটা দিয়েই আমরা কিছু গণনা করতে শুরু করি।
The photos are taken from internet and the data sources are-
- wikipedia.org;
- towardsdatascience.com/what-is-benfords-law;
- mathworld.wolfram.com;
- insights.sei.cmu.edu/blog;
- brilliant.org/benfords-law.
শিক্ষাবর্ষঃ ২০১৯-২০